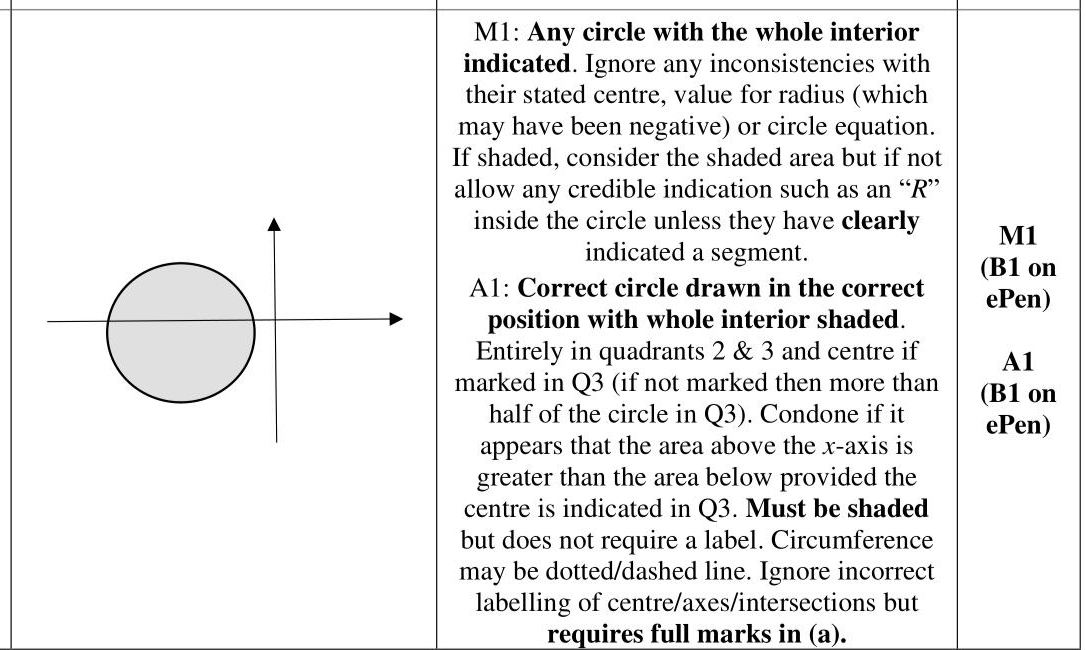
A transformation $$\(T\)$$ from the $$\(z\)$$-plane, where $$\(z=x+\mathrm{i} y\)$$, to the $$\(w\)$$-plane, where $$\(w=u+\mathrm{i} v\)$$ is given by $$\[ w=\frac{z-3}{2 \mathrm{i}-z} \quad z \neq 2 \mathrm{i} \]$$ The line in the $$\(z\)$$-plane with equation $$\(y=x+3\)$$ is mapped by $$\(T\)$$ onto a circle $$\(C\)$$ in the $$\(w\)$$-plane. The region $$\(y> x+3\)$$ in the $$\(z\)$$-plane is mapped by $$\(T\)$$ onto the region $$\(R\)$$ in the $$\(w\)$$-plane. (b) On a single Argand diagram (i) sketch the circle $$\(C\)$$ (ii) shade and label the region $$\(R\)$$ (2)

Answer:

Knowledge points:

Solution: