The random variable $$\(X\)$$ has probability generating function $$\(\mathrm{G}_{X}(t)\)$$ given by $$\[ \mathrm{G}_{X}(t)=\frac{1}{5}+p t+q t^{2}, \]$$ where $$\(p\)$$ and $$\(q\)$$ are constants. Given that $$\(\mathrm{E}(X)=1.1\)$$, find the numerical value of $$\(\operatorname{Var}(X)\)$$. ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . ........................................................................................................................................................ . The random variable $$\(Y\)$$ has probability generating function $$\(\mathrm{G}_{Y}(t)\)$$ given by $$\[ \mathrm{G}_{Y}(t)=\frac{2}{3} t\left(1+\frac{1}{2} t^{2}\right) . \]$$ The random variable $$\(Z\)$$ is the sum of independent observations of $$\(X\)$$ and $$\(Y\)$$.

Answer:

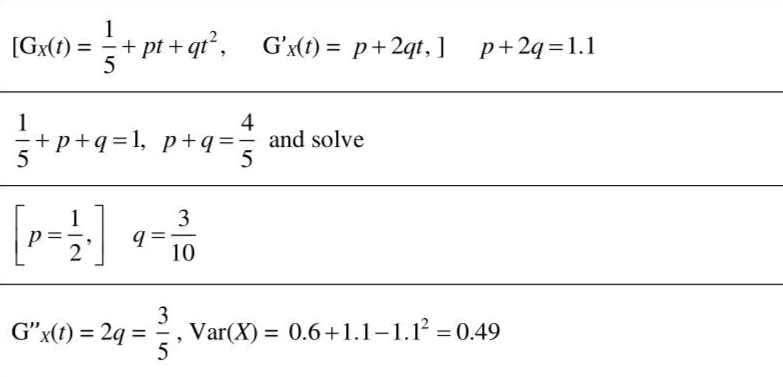
Knowledge points:

Solution: