A scientist is investigating the lengths of the leaves of a certain type of plant. The scientist assumes that the lengths of the leaves of this type of plant are normally distributed. He measures the lengths, $$\(x \mathrm{~cm}\)$$, of the leaves of a random sample of 8 plants of this type. His results are as follows. $$\[ \begin{array}{llllllll} 3.5 & 4.2 & 3.8 & 5.2 & 2.9 & 3.7 & 4.1 & 3.2 \end{array} \]$$ Find a $$\(90 \%\)$$ confidence interval for the population mean length of leaves of this type of plant. ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ . ................................................................................................................................................................ .

Answer:

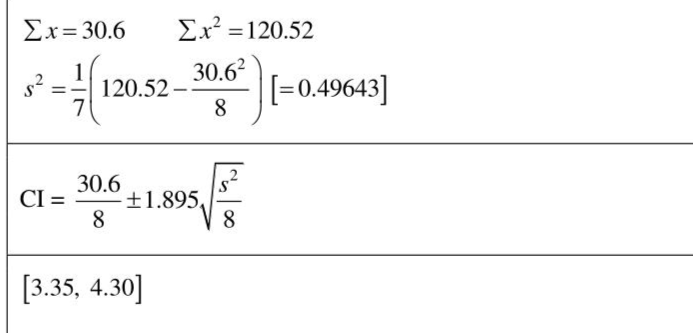
Knowledge points:

Solution: